Related publication: Kosuke Takiguchi, Le Duc Anh, Takahiro Chiba, Harunori Shiratani, Ryota Fukuzawa, Takuji Takahashi and Masaaki Tanaka, “Giant gate-controlled odd-parity magnetoresistance in one-dimensional channels with a magnetic proximity effect”, Nature Comm. 13, 6538 (2022).
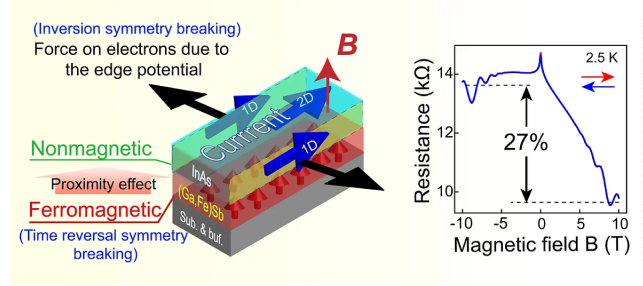
According to Onsager’s principle, electrical resistance R of general conductors behaves as an even function of external magnetic field B. Only in special circumstances, which involve time reversal symmetry (TRS) broken by ferromagnetism, the odd component of R against B is observed. This unusual phenomenon, called odd-parity magnetoresistance (OMR), was hitherto subtle (< 2%) and hard to control by external means. Moreover, the OMR can only occur if and only if the magnetization M and the external magnetic field B are not collinear, which is usually at a small magnetic field range, because the reversal of both M and B reserves the TRS.
However, our recent work upheld this conventional thoughts. In InAs/GaFeSb bilayer strutures, we found a striking OMR of ~27%, which linearly depends on B up to very high field (~ 10 T). InAs is a non-magnetic semiconductor, while GaFeSb is a unique ferromagnetic semiconductor developed in our group. GaFeSb maintains the ferromagnetic order even at room temperature and is very insulating comparing with InAs. There is a strong magnetic proximity effect from GaFeSb to InAs, which breaks TRS in the InAs channel and induces a splitting energy between spin-up and spin-down electrons [1].
There are two unique aspects of our OMR that make it stand out of all the previously reported B-odd magnetoresistances:
1. Our OMR does not depend on the current direction. This indicates that it is not a non-reciprocal transport phenomenon, which was observed in the non-linear response region [2–5] .
2. Our OMR appears even when the magnetic field B is parallel to the magnetization M (B//M). This is completely different from other linear MR phenomena [6–10] (observed in the linear response region), where B and M must be non-collinear.
Thus, the theoretical models proposed thus far to describe the B-odd components of magnetoresistance such as the unidirectional MR (observed in the non-linear response region) [2–5] and linear MR [6–10] (observed in the linear response region) cannot explain the new OMR observed in our study. The results were both exciting and puzzling, to us and to the community as well.
We first made an observation of the OMR in 2018, but was hesitate to publish as it is too large to be expected from a semiconductor system. One of the first thoughts was that whether a Hall resistance component may be accidentally detected in the four-terminal resistance measurement setup. Follow-up experiments excluded this possibility, as the OMR and the Hall resistance, when being controlled by a gate voltage or changing the current, show completely different behaviors. It took us almost 4 years, through various dicussions within the group and with the reviewers, to come up with a reasonable explanation.
Is it a Hall component? Follow-up experiments clearly excluded this possibility.
Hidden channels at the edge
There are two important points deduced directly from our experimental results and careful considerations on the mechanism of our OMR:
-
First, the coupling between the edge-center channels plays a vital role in inducing the new OMR, which is deduced from the following experimental facts:
– The OMR occurs at the edge transport of the InAs layer, which is evident from its absence in the two-terminal measurement and its opposite signs when measured along the opposite edges.
– The OMR requires a magnetic proximity effect from (Ga,Fe)Sb to InAs, as demonstrated by the global gate control experiment. The magnetic coupling at the (Ga,Fe)Sb/InAs interface, however, occurs mainly in the center region (2D channel) of the InAs layer. This is evident in the absence and appearance of a Kondo-like tail at T < ~10 K in the temperature dependence of the resistance of the edge (1D) and center (2D) channels.
-
Second, OMR will appear if there is asymmetry in the scattering rate of electron carriers with different spins in this edge channels. This was straightforwardly deduced from the 1D Hamiltonian of the edge channel and the Boltzmann’s formalism.
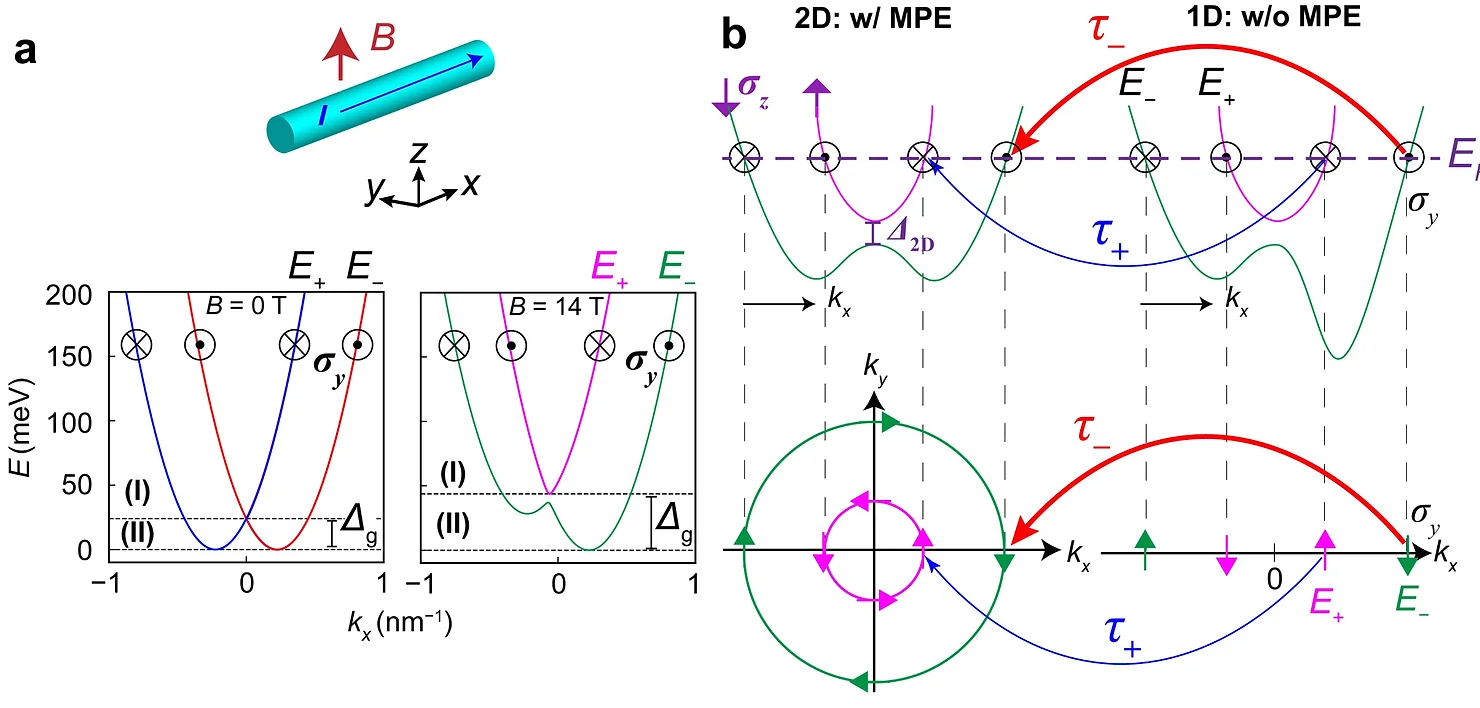
In our proposed model, we figure out that for the electron carriers both in the center and the edges of InAs, spin and momentum should be locked due to the Rashba spin-orbit coupling, a phenomenon commonly known as spin-momentum locking effect. Due to this effect, energy dispersion relation of electron carriers are divided into two brands (E+ and E-), which are characterized by opposite spin – momentum locking directions (chiralities). There will be asymmetry in the scattering rate of electrons in the E+ and E- branches if we assume that this chirality is reserved in the edge-center scattering of InAs. This leads to the appearance of the OMR.
Our theoretical model expects that
(i) OMR in InAs/(Ga,Fe)Sb emerges even when B//M.
(ii) OMR in InAs/(Ga,Fe)Sb is not affected by reversing the current direction.
(iii) OMR in InAs/(Ga,Fe)Sb can be modulated by varying the magnetic proximity effect.
These notable features are indeed confirmed by our experimental results!
Most of the responses are very impressive and convincing. Although I am still not fully convinced in some issues, specifically in theory part, I believed that the experimental setup and results are well presented now and the phenomena found in this work is indeed interesting and is necessary to be further investigated. So I am glad to recommend the publication of the paper in its current form and I hope this publication may bring interest to the researchers in the various fields… (From a reviewer’s comments)
At this stage, our model based on the chirality-dependent scattering between the edge (1D) and center (2D) channels is the first theoretical model that can explain all the aspects of this new OMR. It is challenging to directly verify the chirality-dependent scattering from the present experimental setup, because the spin-orbit coupling cannot be changed independently of other parameters such as carrier density or magnetic proximity effect. However, given the uniqueness and novelty, as well as the possibility of device applications of our observed new OMR, we think that these results are compelling and it is expected that more sophisticated theories will follow in the near future. We are glad that the reviewers share this view with us!
What to expect?
Our results highlight the abundance of new physics in solid state systems when TRS and SIS are simultaneously broken even in well-known materials such as InAs. The linear OMR presented in this work can be applied to magnetic field sensors which provides a large dynamic range (0−10 T) owing to its linearity. This new type of sensors can work at room temperature, requires only simple DC measurements for detection, and its sensitivity can be further enhanced by material engineering, such as optimizing the carrier concentration and SOI strength.
Another exciting point is to figure out the nature of the edge channels. Are they 1D, or quasi-2D? What kind of electrical transport? All are lying ahead waiting to be explored! And we are eager to conquer this quest.
References
[1] Takiguchi, K. et al. Giant gate-controlled proximity magnetoresistance in semiconductor-based ferromagnetic–non-magnetic bilayers. Nat. Phys.15, 1134–1139 (2019).
[2] Tokura, Y. & Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 9, 3740 (2018).
[3] Zhang, S. S. L. & Vignale, G. Theory of unidirectional spin Hall magnetoresistance in heavy-metal/ferromagnetic-metal bilayers. Phys. Rev. B 94, 140411(R) (2016).
[4] Rikken, G. L. J. A., Fölling, J. & Wyder, P. Electrical magnetochiral anisotropy. Phys. Rev. Lett. 87, 236602 (2001).
[5] Rikken, G. L. J. A. & Wyder, P. Magnetoelectric anisotropy in diffusive transport. Phys. Rev. Lett. 94, 016601 (2005).
[6] Singha, R., Satpati, B. & Mandal, P. Fermi surface topology and signature of surface Dirac nodes in LaBi. Sci. Rep. 7, 6321 (2017).
[7] Abrikosov, A. A. Quantum linear magnetoresistance; solution of an old mystery. J. Phys. A. Math. Gen. 36, 9119–9131 (2003).
[8] Abrikosov, A. Quantum magnetoresistance. Phys. Rev. B 58, 2788–2794 (1998).
[9] Xiao, C. et al. Linear magnetoresistance induced by intra-scattering semiclassics of Bloch electrons. Phys. Rev. B 101, 201410 (2020).
[10] Zyuzin, V. A. Linear magnetoconductivity in magnetic metals. Phys. Rev. B 104, L140407 (2021).
